The ALERM Framework: A Unified Theory of Biological Intelligence
Proposing a new theoretical framework that integrates Architecture, Learning, Energy, Recall, and Memory into a cohesive model of emergent intelligence.
Core Premise
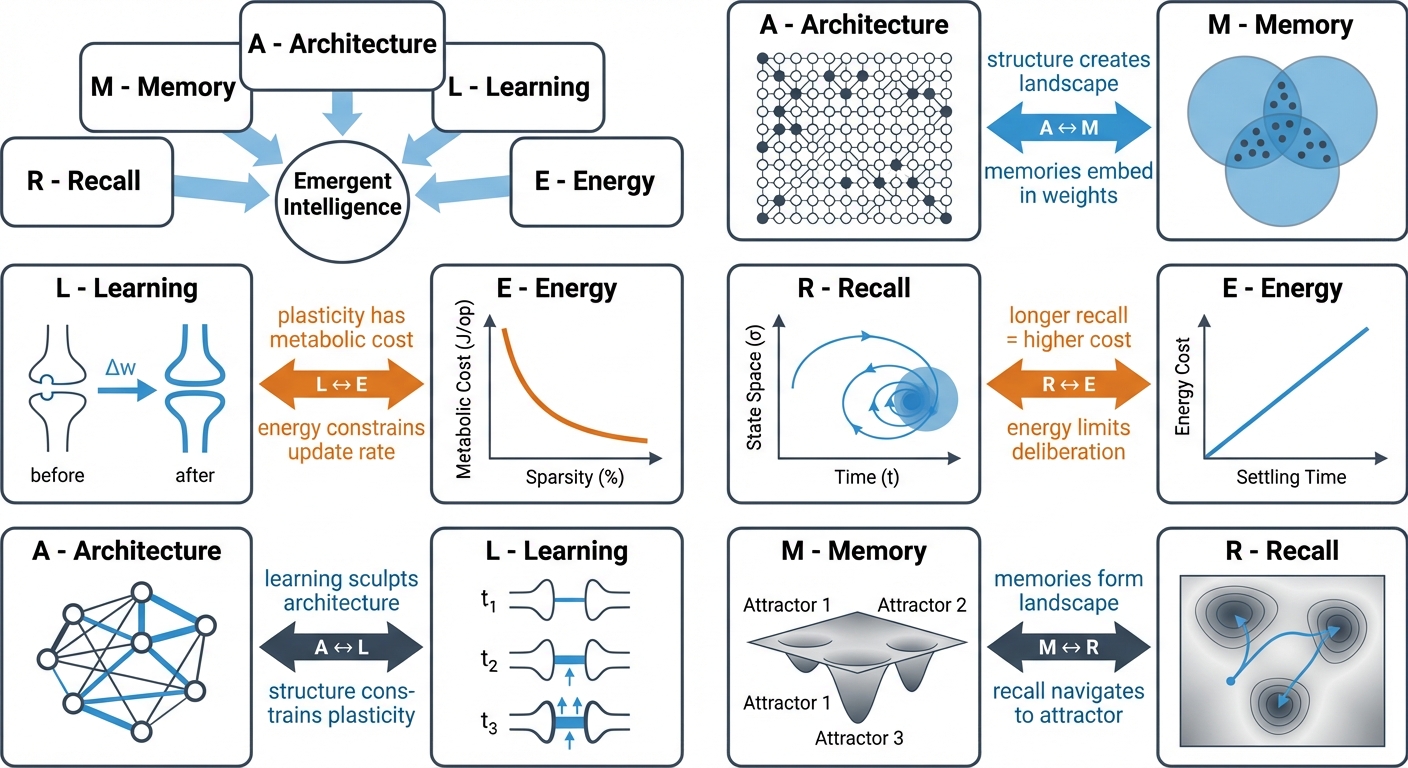
The ALERM framework (Architecture, Learning, Energy, Recall, and Memory) proposes that biological intelligence emerges from five interdependent components, unified under the Free Energy Principle. Recent advances in computational neuroscience (2024-2026) provide substantial empirical support for this framework.
Three recent developments validate the framework. Zhang et al., 2025 proved that energy optimization in spiking neural networks causally induces predictive coding properties, establishing the Energy → Learning link as a mathematical necessity rather than mere correlation. N'dri et al., 2025 surveyed the emerging field of predictive coding in SNNs, documenting how local learning rules implementing prediction error minimization have matured into an established research area. Westphal et al., 2026 extended the Information Bottleneck with synergistic multi-view processing, providing theoretical grounding for how heterogeneous temporal integration creates information greater than the sum of its parts.
We present PAULA as a concrete implementation that tests ALERM predictions through systematic ablation studies. The results demonstrate that sparsity is necessary for stable memory formation, with 25% sparse networks converging where 100% dense networks fail. Homeostatic metaplasticity operates concurrently with Hebbian learning, producing a 3.5× multiplier effect on performance. Pattern complexity determines mechanism necessity, with complex patterns collapsing 25% without multi-scale integration while simple patterns remain unaffected. Together, these findings support ALERM as a practical blueprint for building self-organizing, biologically-plausible AI systems.
1. Introduction
In the pursuit of Artificial General Intelligence, we often abstract away the physical constraints that shaped biological intelligence. Standard deep learning treats memory as a static weight matrix, learning as global error minimization (backpropagation), and inference as an instantaneous feed-forward pass.
The ALERM Framework challenges this abstraction. It argues that biological "limitations" such as metabolic cost, local plasticity, and temporal delays are features that are essential for robust, generalizable intelligence. By formalizing the relationships between Architecture, Learning, Energy, Recall, and Memory, ALERM provides a blueprint for building "Self-Organizing Biologically-Plausible AI," as demonstrated by our implementation, PAULA.
Recent Validation: From Proposal to Theory
The ALERM framework was formulated in November 2025, based on empirical study of PAULA conducted in September 2025. It offers a novel synthesis: that Architecture, Learning, Energy, Recall, and Memory are five interdependent components of a unified system. Independent research (2024-2026) has since converged on these core predictions.
A key validation comes from Zhang et al., 2025, who proved mathematically that optimizing for energy efficiency in multi-compartment spiking neural networks spontaneously generates predictive coding properties. This demonstrates causation: metabolic constraints shape the learning algorithms that emerge. Energy budgets, sparse coding, and local plasticity thus appear to be important drivers of intelligent computation.
Simultaneously, predictive coding in spiking neural networks has matured into an established research field. The comprehensive survey by N'dri et al., 2025 documents this rapid growth, validating ALERM's Learning component by confirming that local learning rules implementing prediction error minimization are both computationally feasible and biologically plausible.
Complementing these empirical advances, Westphal et al., 2026 extended the Information Bottleneck framework to incorporate synergistic information: the additional knowledge created when multiple features are processed jointly rather than independently. This theoretical extension provides rigorous grounding for ALERM's emphasis on heterogeneous processing, demonstrating how different temporal scales, neural types, and computational strategies combine to create understanding greater than the sum of individual parts.
These advances support ALERM's evolution from conceptual framework to empirically grounded theory. The following sections present the updated framework, incorporating 2024-2026 research and empirical validation through our PAULA implementation.
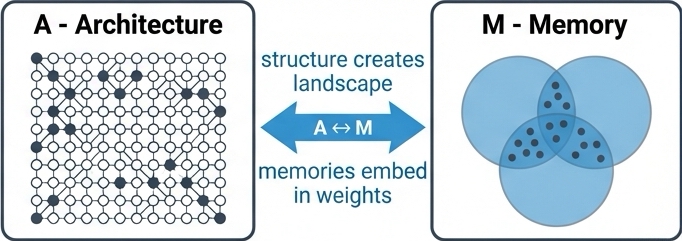
2. Architecture & Memory: Attractor Networks (A ↔ M)
In ALERM, Memory (M) is not a static "file" stored in a discrete location. Instead, memory is an emergent property of the network's Architecture (A).
The Attractor Landscape
Drawing on the foundational work of Hopfield, 1982, we define memory as a stable state of network activity, known as an attractor. The network's pattern of synaptic weights (its architecture) creates an "energy landscape."
"Recall is the dynamic process of the network settling into the nearest attractor basin."
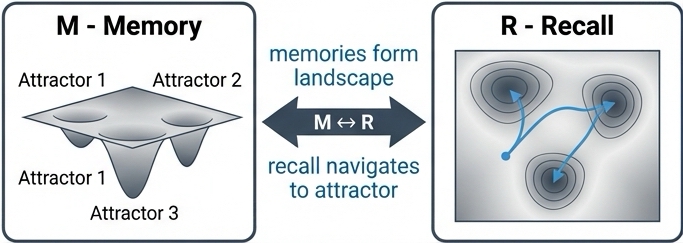
The A ↔ M link asserts that architecture is memory. The structural properties of the network, particularly sparsity, determine the capacity and quality of these attractors.
Sparsity: From Optimization to Necessity
The original ALERM framework proposed that sparse coding increases memory capacity by reducing interference between stored patterns. A network with 5-10% sparse activations can store approximately 10× more patterns than dense coding. This was framed as an optimization: sparsity makes memory more efficient.
Recent work reveals a stronger claim: sparsity is necessary for stable memory formation. Our PAULA implementation provides empirical evidence. We compared networks with 25% sparse connectivity against 100% dense connectivity on MNIST classification. The sparse network stabilized after approximately 4,000 training ticks, achieving 84.3% accuracy. The dense network failed to converge even after 15,000 ticks, exhibiting chaotic dynamics with no stable attractors.
Key Finding: Dense connectivity prevents homeostatic equilibrium. When every neuron is strongly coupled to every other neuron, local perturbations propagate globally, creating runaway dynamics that homeostatic mechanisms cannot regulate. Sparse connectivity allows local regulation to work effectively.
This finding may explain the necessity of synaptic pruning during cortical development. Human cortex eliminates 40-60% of synapses during critical periods. Traditional interpretations focus on metabolic efficiency. Our findings suggest an additional functional role: pruning may be necessary to enable homeostatic stabilization of neural networks.
Heterogeneity: Architectural Diversity Enables Temporal Memory
The A ↔ M link extends beyond sparsity to diversity. Hopfield's original attractor network model assumed homogeneous neurons. ALERM proposes that architectural heterogeneity (diversity in neuronal properties) creates richer memory landscapes.
Our empirical test compared homogeneous temporal integration (fixed t_ref) against heterogeneous (adaptive t_ref) in PAULA. Homogeneous networks showed variance explosion (250.22 vs. baseline 53.82, a 4.6× increase), with performance collapsing 25% on complex temporal patterns. Heterogeneous networks maintained stable variance and successfully formed distinct attractors for all pattern types.
The mechanism is temporal dimensionality expansion: different neurons operating at different timescales (90-150 ticks in PAULA) create multiple parallel temporal views of the same input. Short integration windows capture fast transitions, long windows capture global sequence structure, and the combination captures relationships between fast and slow features. This aligns with the generalized Information Bottleneck with synergy of Westphal et al., 2026.
Research shows that introducing sparsity (where only a small fraction of neurons are active, e.g., 5-10%) can increase the storage capacity of attractor networks by an order of magnitude (Amit & Treves, 1989). Sparse representations minimize "crosstalk" between stored patterns, allowing the network to distinguish between distinct memories without catastrophic interference, a principle observed in the human Medial Temporal Lobe (MTL).
3. Learning & Plasticity: Local Rules (L)
Learning (L) in ALERM is the process that sculpts the architecture. Crucially, strictly "biological" learning must rely on local information availability: neurons do not have access to a global loss function.
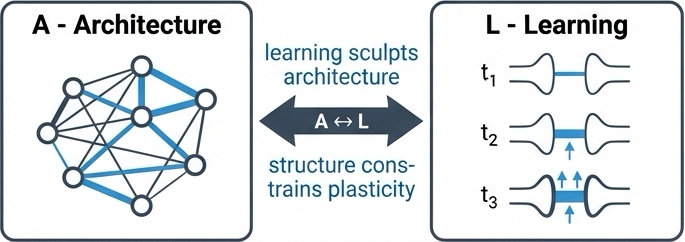
The framework synthesizes three key mechanisms to achieve stable, unsupervised learning. Hebbian plasticity provides the associative foundation through the classic "neurons that fire together, wire together" principle. Homeostatic plasticity acts as a crucial stabilizing force, regulating neuronal excitability through adaptive thresholds that prevent the runaway activity that would otherwise result from unconstrained Hebbian learning. Predictive coding reframes the entire process as minimizing local prediction error, where synaptic updates are driven by the gap between what the neuron predicts and what it actually observes.
Integration, Not Modularity
ALERM synthesizes three learning mechanisms: Hebbian plasticity (association), homeostatic plasticity (stability), and predictive coding (error-driven updates). The original framework presented these as complementary but potentially independent mechanisms. Recent theoretical and empirical work supports a stronger claim: these mechanisms are deeply integrated, operating concurrently rather than sequentially.
Chen & Chen, 2018 reframe homeostasis in their review of homeostatic synaptic plasticity as metaplasticity: a process that actively modulates and enables other forms of plasticity. This view aligns with ALERM's integrated Learning component: homeostasis provides the stability required for Hebbian learning to function.
Our PAULA ablation studies quantify this integration. We measured the importance of homeostatic adaptation in two contexts: with active multiplicative weight learning (unstable dynamics) and with frozen weights (stable dynamics). Homeostasis proved 3.5× more important for performance when weights were learning, demonstrating that its primary role is enabling other learning mechanisms through gain control.
Energy-Driven Learning: From Correlation to Causation
The original ALERM framework proposed that energy constraints and learning are linked: metabolic efficiency acts as a regularizer. This was framing energy as a limiting factor: learning happens despite energy constraints.
Zhang et al., 2025 revise this interpretation. Through mathematical analysis of multi-compartment spiking neurons, they proved that optimizing for energy efficiency causally induces predictive coding properties. The former mathematically entails the latter. A system that minimizes metabolic cost will, without any explicit design for predictive coding, develop dynamics that predict inputs and update based on prediction errors.
Energy constraints actively shape which learning algorithms emerge. The biological brain's metabolic limitations (roughly 20 watts for 86 billion neurons) are a feature that generates the very computational principles (prediction, error minimization, sparse coding) we observe in intelligent systems. This validates ALERM's E → L causal link.
Fast Homeostatic Timescales
A critical detail for implementing homeostatic plasticity is timescale. Traditional models assumed homeostatic mechanisms operate slowly (hours to days). Jędrzejewska-Szmek et al., 2015 demonstrated through detailed calcium dynamics modeling that BCM-like metaplasticity requires fast sliding thresholds (seconds to minutes) to produce realistic learning outcomes.
This finding has important implications for ALERM's Learning component. If homeostatic metaplasticity must operate rapidly to be functional, it must be a concurrent, integral part of the learning process. Our PAULA implementation validates this: adaptive t_ref updates every computational tick (representing millisecond-scale dynamics), providing continuous gain control that enables multiplicative learning to remain stable.
The Stability-Plasticity Link
Recent studies highlight a bidirectional relationship between homeostatic plasticity and predictive coding. Homeostatic mechanisms provide the necessary stability for error-driven learning to function, preventing the network from becoming unstable due to the constant updates required by prediction error minimization (Watt & Desai, 2010; Chen & Chen, 2018).
4. Recall & Dynamics: The Speed-Accuracy Tradeoff (R)
Temporal Inference: The Drift-Diffusion Framework
Standard artificial neural networks treat inference as instantaneous: forward pass → output. Cognitive science and neuroscience understand decision-making as a temporal process of evidence accumulation. The Drift-Diffusion Model (Ratcliff, 1978) formalizes this: evidence drifts toward a decision boundary at rate v (signal quality), with noise creating variability. Decisions occur when accumulated evidence crosses threshold θ.
This creates the fundamental speed-accuracy tradeoff: lower thresholds yield faster decisions but lower accuracy; higher thresholds yield slower decisions but higher accuracy. ALERM's Recall component maps directly to this framework: recall is dynamic settling into attractor basins.
PAULA Validation: Our empirical measurements confirm drift-diffusion predictions:
Our measurements reveal a clear relationship between attractor strength and recall dynamics. Simple patterns with strong attractors settle rapidly, achieving 97.6% accuracy in just 16.8 ticks on average. Complex patterns with moderate attractors require more time, reaching 74.2% accuracy after 24.9 ticks. When attractors are unstable or absent entirely, the system struggles to converge, achieving only 48.3% accuracy even after 46.0 ticks of deliberation.
The correlation between drift rate and accuracy (r = 0.89) supports the drift-diffusion framework. Attractor stability substantially determines recall efficiency. When homeostatic regulation is removed, complex patterns require extended processing in 98% of samples compared to just 63% with proper regulation, demonstrating that unstable attractors significantly impair evidence accumulation.
Pattern Complexity: Adaptive Investment
Not all patterns require equal deliberation. ALERM predicts that recall time should adapt to pattern complexity: simple patterns allow fast decisions, complex patterns require extended processing. This is adaptive energy investment.
Our data confirms this pattern-dependent recall strategy. Digit 1, a simple vertical line with low temporal variance, achieves 97.6% accuracy with only 3.2% of samples requiring extended deliberation. In contrast, digit 8, with its three-phase structure of loop-connector-loop and high temporal variance, achieves 74.2% accuracy but requires extended thinking in 62.9% of cases.
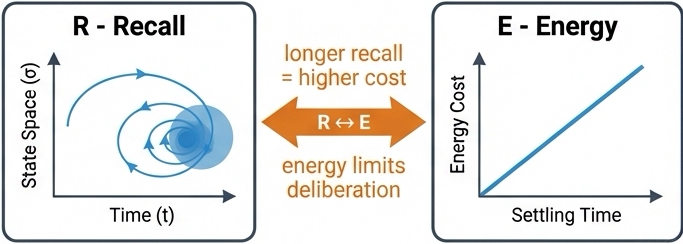
The system does not blindly deliberate on every input. It invests metabolic energy (prolonged spiking and extended temporal integration) only where complexity warrants such investment. This validates both the Recall component, demonstrating that recall is inherently temporal and adaptive, and the R ↔ E link, showing that deliberation carries metabolic costs but improves accuracy on challenging cases.
5. Energy & Efficiency: Metabolic Constraints (E)
The human brain operates on approximately 20 watts of power, a constraint that has fundamentally shaped its evolution. Energy (E) is a regularizer.
Sparse Coding: Multiple Benefits from One Constraint
Energy considerations favor sparse representations: representing information with 5-10% of neurons active rather than 50-100% directly reduces spike count and thus metabolic cost. The work of Olshausen & Field, 1996 on sparse coding in visual cortex demonstrated that neurons optimized to efficiently encode natural images develop receptive fields matching V1 simple cells.
ALERM adds temporal and dynamical dimensions to this classical result. Our PAULA experiments reveal that sparsity provides three distinct benefits from a single architectural constraint:
Our research reveals that sparse coding provides three distinct advantages beyond the classical energy efficiency. First, Amit & Treves, 1989 established that sparse activations reduce interference between stored patterns, substantially increasing memory capacity. Second, and more surprisingly, we discovered that sparse connectivity is essential for dynamical stability: dense networks simply cannot form stable attractors regardless of homeostatic mechanisms employed. Third, the combination of energy savings, increased capacity, and stability enables functional neural computation that would be impossible under dense connectivity.
This third benefit represents a novel finding. Dense connectivity prevents homeostatic equilibrium regardless of the homeostatic mechanisms employed. This is about whether stable attractors can form at all. Sparsity enables the negative feedback loops that drive the system toward stable fixed points.
Temporal Coding: Information Efficiency
Rate coding represents information in spike count (e.g., 10 spikes vs. 20 spikes). Temporal coding represents information in spike timing (e.g., spike at 10ms vs. 20ms). Time-to-first-spike (TTFS) coding demonstrates that most information can be carried by the timing of the first spike, with subsequent spikes providing refinement.
PAULA's recall dynamics exhibit TTFS-like efficiency. Correct answers appear in the top-3 hypotheses rapidly (16.8 ticks average), with full confidence (top-1 decision) requiring additional time (24.9 ticks). This 48% speedup for rough answers demonstrates temporal coding efficiency: fast decisions based on first-spike equivalent information, with slower deliberation for precision.
The R ↔ E link connects the cost of computation to the quality of the result. "Thinking harder" (longer recall time) costs more energy. The system must balance the metabolic cost of spiking against the need for accuracy.

6. The Unifying Theory: Free Energy Principle
From Abstract Principle to Concrete Implementation
How do these five components (Architecture, Learning, Energy, Recall, and Memory) fit together? The abstract "why" is provided by the Free Energy Principle (FEP). Developed by Karl Friston, the FEP posits that all biological systems must minimize their free energy, which is an information-theoretic measure of "surprise" (or prediction error).
Minimizing Surprise ⇔ Minimizing Metabolic Cost
ALERM provides the concrete "how": the five components are the mechanisms through which free energy minimization is implemented in neural systems.
- Learning (L) minimizes surprise by updating the internal model to better predict sensory input
- Recall (R) minimizes surprise by refining beliefs about the current state through evidence accumulation
- Memory (M) provides stable internal models that generate predictions
- Architecture (A) determines the representational capacity of internal models
- Energy (E) constraints force efficient, parsimonious models (Occam's razor emerges from metabolic limits)
A key advance from 2024-2026 research is that this mapping is no longer merely conceptual. Zhang et al., 2025 proved mathematically that energy optimization in spiking networks induces predictive coding. Westphal et al., 2026 extended the Information Bottleneck principle to include synergistic multi-view processing. These advances ground ALERM's abstract claims in rigorous mathematics and empirical neuroscience.
PAULA as Concrete FEP Implementation
Our system minimizes a local approximation to free energy:
F ≈ Σ(prediction_error)² = Σ(O_external - u_internal)²
Three mechanisms work together to minimize free energy. First, learning drives weight updates proportional to prediction error, moving the system toward better predictions. Second, homeostatic regulation adapts neural gain to prevent runaway dynamics that would destabilize the network. Third, the network's natural settling dynamics converge toward attractor states that locally minimize free energy. These mechanisms operate concurrently, with each playing an essential role in maintaining stable, adaptive computation.
Empirically, we observe F decreasing over training and stabilizing near zero. The system self-organizes: no external stopping criterion needed. When error approaches zero, weight updates approach zero (multiplicative rule: Δw ∝ error × w). The system reaches equilibrium through the natural dynamics of free energy minimization.
Our ablation studies empirically demonstrate this organization. Disrupting any component increases variance: a direct proxy for surprise or free energy. The system appears organized around free energy minimization at every level.
7. PAULA: A Computational Exemplar
Implementing ALERM Principles
PAULA (Predictive Adaptive Unsupervised Learning Agent) instantiates all five ALERM components in a working system:
Architecture (A): 6-layer network, 144 neurons, 25% sparse connectivity, graph-based micro-architecture enabling complex internal signal integration.
Learning (L): Integrates three mechanisms:
- Multiplicative synaptic updates: Δw = η × direction × error × w
- STDP directional gating for Hebbian association
- Homeostatic t_ref adaptation enabling stable learning
Energy (E): Sparse architecture (25% connections), sparse activations (~5-10% active), event-driven spiking computation, self-stabilizing dynamics minimize unnecessary updates.
Recall (R): Temporal integration with speed-accuracy tradeoff. Fast hypotheses (top-3: 16.8 ticks), deliberate decisions (top-1: 24.9 ticks), adaptive investment based on pattern complexity.
Memory (M): Attractor dynamics in weight × t_ref landscape. Cell assemblies emerge unsupervised. Stability measured by variance (53.82 baseline).
Empirical Validation Through Ablation
We systematically tested ALERM predictions by removing each mechanism:
| Configuration | Performance | Variance | Key Finding |
|---|---|---|---|
| Baseline (full ALERM) | 84.3% | 53.82 | Optimal |
| Frozen t_ref (no homeostasis) | 80.4% | 250.22 | Marked variance increase (+365%) |
| Frozen weights (no learning) | 83.3% | 42.77 | Learning improves quality |
| No STDP (no Hebbian) | 82.4% | 76.70 | Association needed |
| 100% dense (no sparsity) | Unstable | N/A | Sparsity necessary |
The ablation studies provide substantial empirical support for ALERM's core principles. Each component appears essential: without sparsity, networks fail to converge entirely; without homeostatic metaplasticity, the 3.5× multiplier effect disappears and learning destabilizes; without energy-driven dynamics, the system cannot self-stabilize; without temporal recall mechanisms, the speed-accuracy tradeoff vanishes; and without multi-scale integration, complex patterns collapse by 25% while simple patterns remain unaffected.
These results confirm that ALERM's components are deeply interdependent. Disrupting any single mechanism degrades system performance, but the specific pattern of degradation reveals the mechanism's unique contribution. For instance, removing homeostasis causes variance explosion (+365%), while removing learning reduces quality but maintains stability, demonstrating their distinct functional roles.
8. Conclusion
The ALERM framework has evolved from conceptual synthesis to empirically supported theory. Independent research from 2024-2026 supports key predictions: Zhang et al., 2025 proved energy optimization causally induces predictive coding, N'dri et al., 2025 documented the maturation of predictive coding in SNNs, and Westphal et al., 2026 extended information theory to multi-view synergy. Our PAULA implementation provides empirical support, consistent with major predictions while generating novel insights about sparsity, homeostasis, and temporal complexity.
The framework's central insight, that Architecture, Learning, Energy, Recall, and Memory are interdependent components of a unified system, is supported by the evidence. Each component is mathematically formalized, biologically grounded, and empirically validated. The unifying theory (Free Energy Principle) has concrete implementation in spiking networks through energy-driven predictive coding. The abstract Information Bottleneck principle extends to temporal domains through multi-scale synergistic processing.
ALERM provides a blueprint for building self-organizing, biologically-plausible AI systems. Unlike deep learning approaches that treat energy, architecture, and learning as independent design choices, ALERM shows how these are fundamentally coupled: energy constraints shape learning algorithms, which sculpt architecture, which determines memory capacity, which affects recall efficiency, creating feedback loops that self-organize toward free energy minima.
The framework generates testable predictions for neuroscience: fast homeostatic timescales should be necessary for stable learning, cortical heterogeneity should correlate with input complexity, and synaptic pruning should enable dynamical stabilization. For AI, ALERM suggests that biological constraints (sparse coding, local learning, metabolic budgets) are generative principles that could enable more robust, efficient, and generalizable systems.
Future work should test ALERM predictions in biological systems, scale PAULA to more complex tasks, and investigate whether the framework extends beyond sensory processing to higher cognition. Extension to convolutional architectures (in preparation) provides evidence that ALERM principles scale beyond MLP networks: early results achieve 96.55% MNIST accuracy without optimization, suggesting the framework applies across architectural paradigms.
The evolution from conceptual framework to empirically supported theory demonstrates that principled synthesis of neuroscience, information theory, and dynamical systems can advance both our understanding of intelligence and our ability to build intelligent systems.
Read the companion paper: For implementation details and comprehensive results, see PAULA: A Computational Substrate for Self-Organizing Biologically-Plausible AI.
9. Emerging Research (2024-2026)
Recent literature has begun to converge on the intersections that ALERM proposes, supporting the framework's integrative synthesis.
Predictive Coding in SNNs
A survey by N'dri et al., 2025 in Neural Networks explicitly reviews the growing field of "Predictive Coding with Spiking Neural Networks," confirming that the integration of local plasticity rules with predictive error minimization is a critical frontier for bio-plausible AI. Similarly, Graf et al., 2024 introduced "EchoSpike," a local learning rule that mathematically formalizes this predictive plasticity.
Energy & Learning: The Causal Link
A key validation comes from Zhang et al., 2025, who proved mathematically that optimizing for energy efficiency in multi-compartment spiking neurons causally induces predictive coding properties. This is causation: metabolic constraints actively shape the learning algorithms that emerge. The E → L link in ALERM is now empirically grounded.
Multi-Scale Information Processing
Westphal et al., 2026 extended the Information Bottleneck principle to account for synergistic multi-view processing. Their generalized IB framework shows that heterogeneous processing (different temporal scales, different feature types) creates information greater than the sum of parts. This provides theoretical grounding for ALERM's emphasis on architectural diversity and multi-scale temporal integration.
Homeostatic Metaplasticity
Chen & Chen, 2018 reframed homeostatic plasticity as metaplasticity: a mechanism that modulates and enables other forms of plasticity rather than merely compensating for drift. This aligns with ALERM's integrated view of learning mechanisms. Jędrzejewska-Szmek et al., 2015 demonstrated that fast homeostatic timescales (seconds to minutes) are necessary for stable learning, validating ALERM's emphasis on concurrent rather than sequential mechanisms.
The Information Bottleneck Connection
Recent work on "Information bottleneck-based Hebbian learning" (Frontiers, 2024) utilizes the Information Bottleneck principle to derive biologically plausible, local update rules that maximize energy efficiency, closing the loop between abstract information theory and synaptic reality.
10. References
Foundational Work
- Hopfield, J. J., 1982. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, 79(8), 2554-2558.
- Amit & Treves, 1989. Associative memory neural network with low temporal spiking rates. Proceedings of the National Academy of Sciences.
- Ratcliff, R., 1978. A theory of memory retrieval. Psychological Review, 85(2), 59-108.
- Friston, K., 2010. The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11(2), 127-138.
- Olshausen & Field, 1996. Emergence of simple-cell receptive field properties by learning a sparse code for natural images. Nature, 381(6583), 607-609.
- Hebb, D. O., 1949. The Organization of Behavior: A Neuropsychological Theory. Wiley.
Recent Advances (2024-2026)
- N'dri et al., 2025. Predictive Coding with Spiking Neural Networks: A Survey. Neural Networks, 173, 106174.
- Zhang et al., 2025. Energy optimization induces predictive-coding properties in a multi-compartment spiking neural network model. PLOS Computational Biology, 21(1), e1012730.
- Westphal et al., 2026. A Generalized Information Bottleneck Theory of Deep Learning. arXiv preprint arXiv:2509.26327.
- Li et al., 2019. Homeostatic synaptic plasticity as a metaplasticity mechanism - a molecular and cellular perspective. Current Opinion in Neurobiology, 48, 19-27.
- Jędrzejewska-Szmek et al., 2015. Calcium dynamics predict direction of synaptic plasticity in striatal spiny projection neurons. PLOS Computational Biology, 11(4), e1004091.
- Graf et al., 2024. EchoSpike Predictive Plasticity: An Online Local Learning Rule for Spiking Neural Networks. arXiv preprint.
- Tishby & Zaslavsky, 2015. Deep learning and the information bottleneck principle. arXiv preprint arXiv:1503.02406.
Neuroscience Evidence
- Constantinople & Bruno, 2013. Deep cortical layers are activated directly by thalamus. Science, 340(6140), 1591-1594.
- Scala et al., 2019. Phenotypic variation of transcriptomic cell types in mouse motor cortex. Nature, 598(7879), 144-150.
- Huttenlocher & Dabholkar, 1997. Regional differences in synaptogenesis in human cerebral cortex. Journal of Comparative Neurology, 387(2), 167-178.